Hello everyone! Welcome to the third part of the public-key cryptography series! In the previous part, the notion of prime number was discussed. This part is intended to give an introduction for public / private key pairs and encryption / decryption by using them. Once again, you'll have the opportunity to apply the math using the provided Rust code.
Contents
Basics of Public-Key Cryptography
What is a key pair?
Private Key
Public Key
How it works?
Real World Applications
Mathematical Foundations
Key Generation Principles & Prime Numbers
Euler's Totient Function
Formula of Secrecy
Encryption / Decryption
From Theory to Hands-on Practice (Rust Code)
Key Generation
Encryption / Decryption
It is time to test!
Conclusion
Basics of Public-Key Cryptography
What is a key pair?
A key pair consists of two keys:
private key and
public key.
Public Key
It is available to everyone and used for encryption. It's like a digital address shared openly for others to send encrypted messages. So, anyone can use a recipient's public key to encrypt a message. Once the message is encrypted, it can only be decrypted by the corresponding private key.
Private Key
It is used for decryption and, as the name suggests, kept secret. The recipient uses their private key to decrypt encrypted messages. The strength of the system lies in the fact that, although the public key is known to all, it is computationally infeasible to derive the private key from it.
How it works?
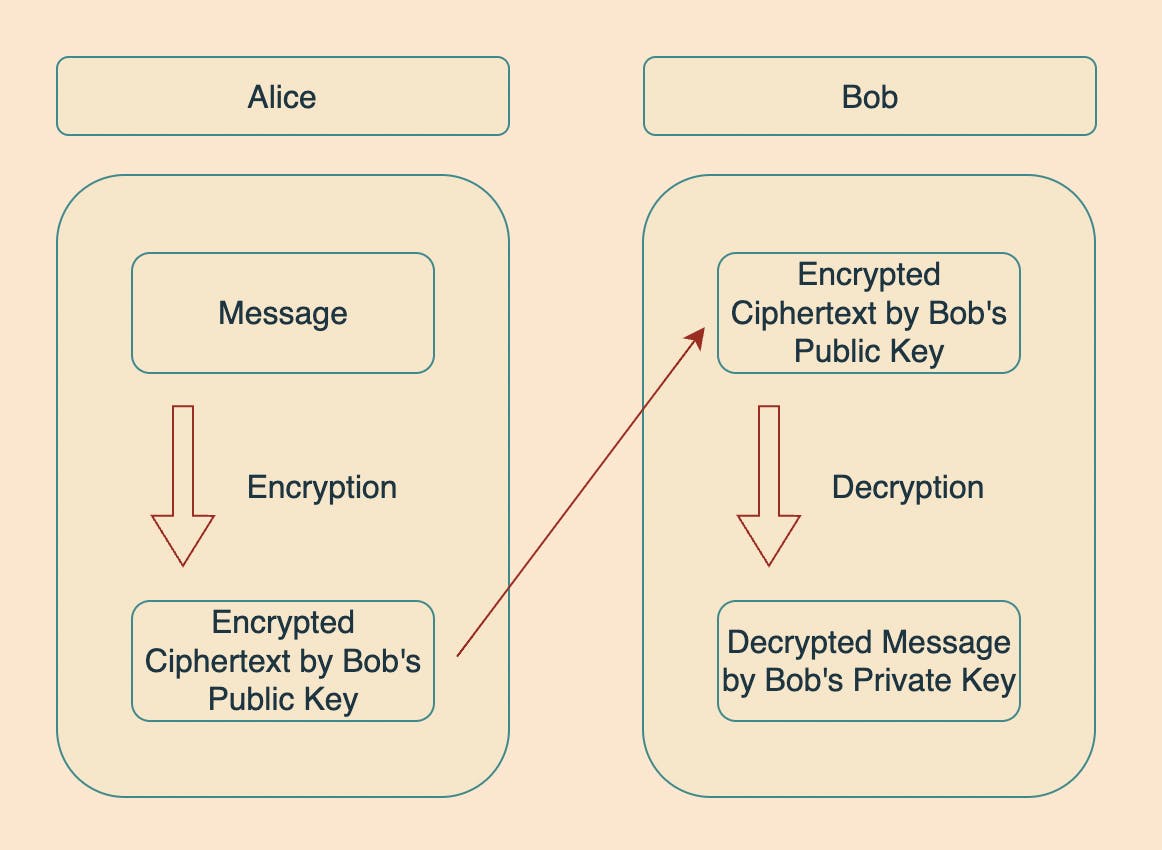
Let's consider a scenario where two close friends, Alice and Bob, wish to communicate secretly. In this situation, Alice and Bob can use public-key cryptography (assuming they have securely shared their keys with each other; we will discuss key sharing methods shortly) to maintain the confidentiality of their messages.
Alice encrypts her message using Bob's public key and sends it over to Bob.
Bob receives the encrypted message, decrypts it using his own private key, and finally reads it.
Real World Applications
Email
Email encryption serves as a technique to protect the contents of email communications from unauthorized access by external parties. When an email is encrypted, it becomes unreadable to any person. Decryption and restoration of the original message are only possible using your unique private email key.
This encryption process utilizes public-key cryptography.
Social media platforms like WhatsApp and Instagram also use public-key cryptography (sometimes private-key cryptography also) for end-to-end encryption.
Blockchains
In almost all the blockchains, public-key cryptography is extensively used.
Where public keys are used as an account number, private keys are used to sign transactions (I will write a particular blog post on digital signatures) and to prove ownership of an address and the assets contained within it.
Mathematical Foundations
In this section, we will discuss the mathematical fundamentals of key generation. You will see that how important prime numbers will be for public-key cryptography.
Key Generation Principles & Prime Numbers
There is more than one approach to key generation in public-key cryptography. Two of them are:
RSA cryptography,
Elliptic curve cryptography.
Although I'm planning another series of posts regarding elliptic curve cryptography, for the sake of simplicity, we will discuss and practice RSA encryption in this series.
RSA encryption relies on prime factorization of large numbers being computationally difficult. We want the calculation to be easy to perform in one direction, but difficult to invert if you don't have the proper key.
So far, we have discussed how public-key cryptography worked, but we never discussed how were those public and private keys generated.
The main principle in generating public / private key pairs is the use of large prime numbers. Recall from the previous post about prime numbers.
Unpredictability: Large primes are not easily guessable, adding a layer of security,
Unique Factorization: The fact that every natural number can be uniquely factored into primes is crucial in algorithms like RSA, where the security relies on the difficulty of factoring the product of two large prime numbers.
Euler's Totient Function
Euler's totient function \(\phi(n)\) is defined as the count of positive integers up to $n$ that are relatively prime to $n$. Simply it calculates the number of integers less than $n$ that do not share any common factors with $n$, except for the number 1.
Calculation
For a Prime Number$p$: \(\phi(p) = p - 1.\) This is because all numbers less than a prime number are coprime to it.
For a Product of Two Primes$p$ and $q$: \(\phi(p \ \times \ q) = (p - 1) \ \times \ (q - 1).\) This results from the fact that none of the numbers less than \(p \ \times \ q\) are divisible by either $p$ or $q$, except for the multiples of $p$ and $q$.
General Case: If \(n = p_1^{k_1} \times p_2^{k_2} \times \ ... \ \times p_r^{k_r}\), where \(p_1, p_2, ..., p_r\) are distinct prime numbers and \(k_1, k_2, ..., k_r\) are their respective powers, then
- \(\phi(n) = n \times (1 - \frac{1}{p_1}) \times (1 - \frac{1}{p_2}) \times \ ... \ \times (1 - \frac{1}{p_r})\).
It is time to construct the key generation algorithm.
For the algorithm to help Bob communicate with Alice, Bob would need to create a public key for Alice to encrypt messages, and a private key to help Bob decrypt Alice's messages. RSA key generation works as follows:
Take two large prime numbers, $p$ and $q$, and multiply them to get a number $N$. Keep $p$ and $q$ secret.
Calculate the totient of $N$: \(\phi(N) = (p-1)(q-1)\).
Find a positive integer $e$ that is less than \(\phi(N)\) and is coprime with \(\phi(N)\), meaning the greatest common divisor (GCD) between $e$ and \(\phi(N)\) is 1.
Calculate the number \(d = e^{-1} \ mod \ \phi(N)\). Notice that this means \(e \cdot d \equiv 1 \ mod \ \phi(N)\), so $d$ and $e$ are modular inverses of one another.
The pair of integers $(N, e)$ represents Bob's public key and can be shared by everyone who wants to communicate with him. Similarly $(N,d)$ represents Bob's private key that is supposed to be kept as a secret.
Encryption / Decryption
Now, if Alice wants to send a message $m$ and encrypt it into ciphertext $c$ to send over to Bob, she would perform the following calculation:
$$Enc(m) = m^{e} \ mod \ N = c.$$
Bob receives the encrypted message and decrypts it by performing the following calculation:
$$Dec(c) = c^{d} \ mod \ N = m.$$
Notice that the aysmmetric encryption correctness property holds:
$$Dec(Enc(m)) = m^{ed} \ mod \ N \equiv m \ mod \ N$$
as $e$ and $d$ are multiplicative inverses of each other.
From Theory to Hands-on Practice (Rust Code)
Key Generation
Before starting to write generate_keys() function, let's recall a slightly modified version of mod_inverse() function we have built in the previous post:
fn mod_inverse(e: u64, phi: u64) -> Option<u64> {
let (mut a, mut b, mut x0, mut x1) = (phi, e, 0u64, 1u64);
while b > 0 {
let q = a / b;
(a, b) = (b, a % b);
(x0, x1) = (x1, x0.wrapping_sub(x1.wrapping_mul(q)));
}
if a > 1 {
None
} else {
Some(x0.wrapping_add(phi) % phi)
}
}
We will also need a new function to calculate modular exponents (to perform an exponentiation over a modulus):
fn mod_exp(mut base: u64, mut exp: u64, modulus: u64) -> u64 {
if modulus == 1 { return 0 }
let mut result = 1;
base %= modulus;
while exp > 0 {
if exp % 2 == 1 { result = result * base % modulus }
exp >>= 1;
base = base * base % modulus;
}
result
}
Now, we are ready to construct the key generation function. It will take the tuple$(p, q)$and will output the triple $(N, e, d)$:
fn generate_keys(p: u64, q: u64) -> (u64, u64, u64) {
}
Let us start by defining the basic variables like
\(N = p \times q\),
\(\phi = (p-1)(q-1)\):
let N = p * q;
let phi = (p - 1) * (q - 1);
The most commonly used value for $e$ in RSA-like systems is 65537 (which is of course a prime number).
let e = 65537;
Now that we have everything we need, all we have to do is calculate $d$ by calculating the modular inverse of $e$ in mod \(\phi\) by ensuring such a modular inverse exists:
let d = mod_inverse(e, phi).expect("Modular inverse does not exist!");
Returning the $(N, e, d)$ triple will complete generate_keys() function:
fn generate_keys(p: u64, q: u64) -> (u64, u64, u64) {
let n = p * q;
let phi = (p - 1) * (q - 1);
let e = 65537;
let d = mod_inverse(e, phi).expect("Modular inverse does not exist.");
(n, e, d)
}
Encryption / Decryption
Let us recall the encryption and decryption functions:
$$Enc(m) = m^{e} \ mod \ N = c. $$
$$Dec(c) = c^{d} \ mod \ N = m.$$
So, all we need for encryption is to have:
fn encrypt(message: u64, e: u64, n: u64) -> u64 {
mod_exp(message, e, n)
}
Similarly, what we need for decryption is to have:
fn decrypt(ciphertext: u64, d: u64, n: u64) -> u64 {
mod_exp(ciphertext, d, n)
}
The code is almost ready. We need to define $p$, $q$, and the message $m$. Normally those primes are extremely large to make the system more complicated. But, for the sake of simplicity, let's choose $p$ and $q$ a bit small, for example:
Of course, there are some restrictions we need to be mindful of:
They are both prime.
\(\phi = (p-1)(q-1) = 3120\) is coprime to \(e = 65537\).
So, we can proceed with these selections. Let's implement it inside the main() function:
fn main() {
let p: u64 = 61;
let q: u64 = 53;
let (n, e, d) = generate_keys(p, q);
let message = 42;
let encrypted = encrypt(message, e, n);
let decrypted = decrypt(encrypted, d, n);
}
It is useful to put some print lines to check if the code is working properly:
fn main() {
let p: u64 = 61;
let q: u64 = 53;
let (n, e, d) = generate_keys(p, q);
println!("Public Key: (e: {}, n: {})", e, n);
println!("Private Key: (d: {}, n: {})", d, n);
let message = 42;
let encrypted = encrypt(message, e, n);
let decrypted = decrypt(encrypted, d, n);
println!("Original message: {}", message);
println!("Encrypted message: {}", encrypted);
println!("Decrypted message: {}", decrypted);
}
It is time to test!
Output:
Public Key: (e: 65537, N: 3233)
Private Key: (d: 2753, N: 3233)
Original message: 42
Encrypted message: 2557
Decrypted message: 42
As you can see, we are able to retrieve the original message after completing the encryption and decryption processes. So our code passed the most fundamental test:
$$Dec(Enc(m)) \equiv m \ mod \ N.$$
You can test this code by yourself on Rust Playground.
Don't forget the coprimality condition when setting the primes $p$ and $q$.
Conclusion
In this post, we have delved deeper into the world of public-key cryptography, exploring the aspects of public and private keys, and how they are used in RSA encryption. We've discussed the importance of prime numbers in generating these keys and touched on Euler's Totient Function, which plays a crucial role in the process. We've also seen how these concepts are applied in real-world scenarios like email, social media, and blockchains. Lastly, we have taken a practical approach by implementing these concepts in Rust code, demonstrating how to generate keys and encrypt and decrypt messages.
I hope this series of posts has been helpful for you. See you in the next post!
